How to Solve Trig Identity Problems with Quadrant Information: A Tutor’s Step-by-Step Guide

Questions involving exact trigonometric values and quadrant information appear frequently on the Manitoba Pre-Calculus Provincial Exam. Students often find these challenging because they require combining reference-triangle reasoning with compound-angle and double-angle identities. As a tutor, I see this type of problem come up often, and mastering it builds confidence for the exam.

Here is an example of a question in this style:

Example

You are given that

cos(α) = −(2 / 3)

and that the angle α lies in the interval [π, 3π/2]

You are also told that

tan(β) = −(2 / 5)

and that the angle β lies between [π/2, π]

Using this information, determine the exact values of:

a) cos(α + β)

b) sin(2α)

Solution to part (a)

Before we begin, recall how trigonometric ratios relate to coordinates on a circle.

Suppose we have:

• a circle centered at the origin (0, 0)

• a point (x, y) lying on the circle, and

• a right triangle formed by:

  • one leg along the x-axis,

  • one leg vertical from (x, y) to the x-axis,

  • and the hypotenuse from the origin to (x, y)

    
    

Let r be the length of this hypotenuse (the distance from the origin to (x, y)). Then:

• sin(θ) = y / r

• cos(θ) = x / r

• tan(θ) = y / x

Step 1: Apply the sum and difference identity formula for cos(α + β)

cos(α + β) = cos(α)cos(β) − sin(α)sin(β)

In the above formula, the only information we know is the exact value for cos(α). We must find the exact value for cos(β), sin(α), and sin(β).

Step 2: Find the other necessary exact value for angle α

Since we know cos(α) = −2 / 3 and that the angle α lies in the interval [π, 3π/2], we can construct a right-angled triangle in quadrant 3 with adjacent side -2 and hypotenuse 3. The adjacent side of −2 must be negative since the x-coordinate is always negative in quadrant 2. The hypotenuse of 3 is always recorded as a positive number. The opposite is currently unknown and labelled as y.

Note that the angle shown is the reference angle for α. We can use SOH CAH TOA with this angle as long as the sign of each side of the triangle is correct (the opposite and adjacent sides should be negative).

To find the opposite side, use SOH CAH TOA

(−2)² + (y)² = (3)²

This implies y = ±√5

Since y must be negative in quadrant 3, we use y = −√5

Hence, sin(α) = −√5 / 3

Step 3: Find the other necessary exact value for angle β

Since we know tan(β) = −(2 / 5) and that the angle β lies between [π/2, π] we can construct a right-angled triangle in quadrant 2 with opposite side 2 and adjacent side −5. The opposite side of 2 must be positive since the y-coordinate is always positive in quadrant 2. The adjacent side of −5 must be negative since the x-coordinate is always negative in quadrant 2. The hypotenuse is currently unknown and labelled as r.

Note that the angle shown is the reference angle for β. We can use SOH CAH TOA with this angle as long as the sign of each side of the triangle is correct (the opposite side should be positive and the adjacent side should be negative).

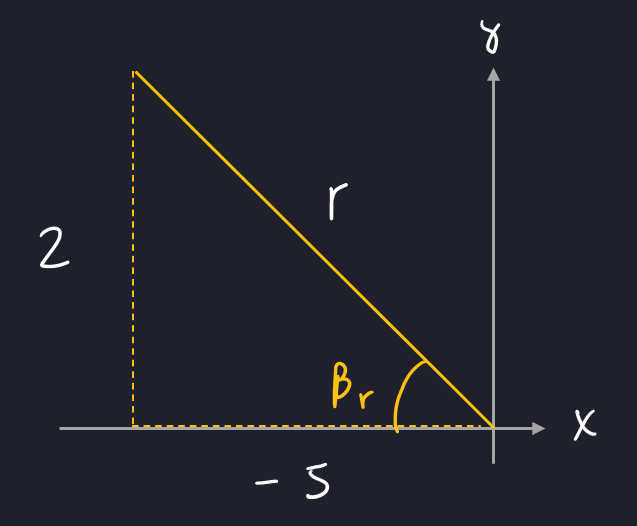
To find the hypotenuse, use SOH CAH TOA

(2)² + (5)² = (r)²

This implies r = ±√29

Since we always treat hypotenuse r as positive, we use r = √29 Hence,

• sin(β) = 2 / √29

• cos(β) = −5 / √29

Step 4: Substitute all the found exact values to find the exact value of cos(α + β)

See the attached image

That is the exact value.

Solution to part (b)

Step 1: Apply the double angle identity formula for sin(2α)

sin(2α) = 2sin(α)cos(α)

Step 2: Substitute all the found exact values to find the exact value of sin(2α)

That is the exact value.

---

Need help with trig identities? If you’re in Winnipeg and looking for a tutor, Tutor Advance provides expert one-on-one support!

---